資料來源:https://starship-knowledge.com
學習以下知識,需要先了解神經元三層結構(Input, Hidden, Output Layer)、激活函數(Activation Function),如果不了解建議先閱讀上一篇文章點我
感知器中的名詞介紹
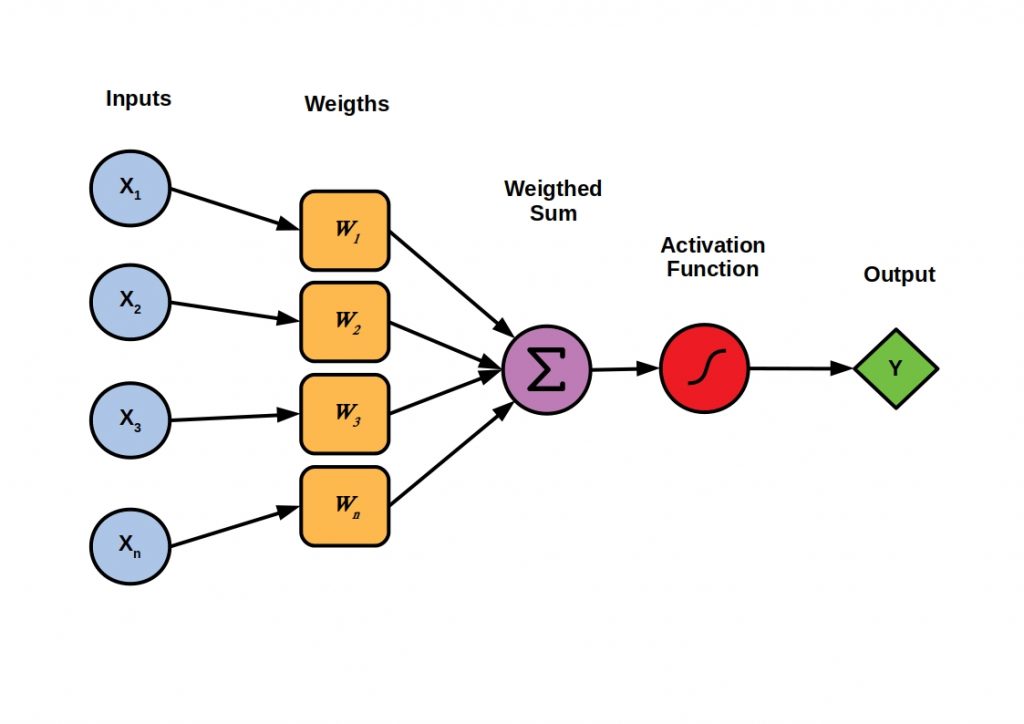
Inputs
這裡的Inputs不代表一定是輸入層(Input Layer),它可以是指任何一層的資料輸入。Inputs可以理解成接收資料特徵。
Weights
中文稱「權重」,每一個連接(Connection)都會有權重,用來決定這個連接的資料輸入值對預測的影響程度,幫助程度越大權重數值越高。
Weighted Sum
中文稱「加權總和」,是將輸入值和權重值相乘。
輸入值 x 權重值 = 加權總和
Output
這裡的Output不代表一定是輸出層(Output Layer),它可以是任何一層的資料輸出。
權重與門檻和輸入的關係
用簡單的例子來了解感知器(Perceptron),x1, x2, x3 ... xn是不同的事,Output是決定要做哪件事,假設x1是要不要出去玩,如果是要x1 = 1,如果是不要x1 = 0,每件事(x)的重視程度都不同,所以每個x都會有相對應的權重(Weight),重視程度越大權重值越高,其實感知器還有一個參數在上圖沒有寫出來,那就是門檻(Threshold),假設重視程度(權重)未達門檻,那都不會成立。
多個感知器形成一個神經網路
每個神經元都會將每個輸入乘以一個權重(數學算式簡稱w)並總和(也就是前面說的加權總和 Weighted Sum),總和值如果大於門檻(數算式稱threshold)則輸出1,相反小於門檻則輸出0。如果神經網路有多個隱藏層(Hidden Layer),下一層神經元就會依照前一層的輸出,在做更複雜的資料處理,也一樣是用感知器這樣的架構。
w1 x x1 + w2 x x2 + w3 x x3 + ... + wn x xn > threshold(門檻)
用數學來解釋Perceptron

資料來源:https://datasciocean.tech
Σ是求和符號,又稱為總和,上圖是將wjxj總和。
j是輸入數據的維度,Σj的j代表有多少個wjxj,wj的j代表有多少個w,xj的j代表有多個x。
不過這樣看起來還是有些複雜,以下是簡化的數學算式:

資料來源:https://datasciocean.tech
這裡多了個+b,b全名是Bias,中文稱「偏差」,權重乘以輸入最後加上偏差。以Sigmoid函式來舉例,假設希望輸出(y)都大於0.5,那麼輸入(x)要大於0才能達成,如果輸入(x)很多都小於0,就可以透過偏差去設置輸入(x)的起始點,讓輸入(x)最小值也在0,映射到輸出(y)就可以大於0.5。

資料來源:https://wikimedia.org
更新
2023/2/3 新增偏差(Bias)的說明